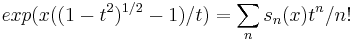Mott polynomials

In mathematics the Mott polynomials s_n(x) are polynomials introduced by N. F. Mott (1932, p. 442) who applied them to a problem in the theory of electrons. They are given by

$exp(x((1-t^2)^{1/2}-1)/t) = \sum_ns_n(x)t^n/n!$

The polynomials s_n(x) form the associated Sheffer sequence for –2t/(1–t²) (Roman 1984, p.130). Arthur Erdélyi, Wilhelm Magnus, and Fritz Oberhettinger et al. (1955, p. 251) give an explicit expression for them in terms of the generalized hypergeometric function ₃F₀.

References

Erdélyi, Arthur; Magnus, Wilhelm; Oberhettinger, Fritz; Tricomi, Francesco G. (1955), Higher transcendental functions. Vol. III, McGraw-Hill Book Company, Inc., New York-Toronto-London, MR 0066496
Mott, N. F. (1932), "The Polarisation of Electrons by Double Scattering", Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character (The Royal Society) 135 (827): 429–458, ISSN 0950-1207, JSTOR 95868
Roman, Steven (1984), The umbral calculus, Pure and Applied Mathematics, 111, London: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], ISBN 978-0-12-594380-2, MR 741185, Reprinted by Dover, 2005, http://books.google.com/books?id=JpHjkhFLfpgC